The latest version of Deepmind's AlphaGeometry system can solve geometry problems better than most human experts, matching the performance of top math competition winners.
AlphaGeometry2 solves 84% of International Mathematical Olympiad (IMO) geometry problems from 2000 to 2024, up from its predecessor's 54%. On the IMO-AG-50 benchmark, which includes 50 formalized IMO geometry problems, it solved 42 problems - slightly better than an average gold medalist, who typically solves around 40.
The system works by pairing two main components: a language model based on the Gemini architecture, and a symbolic engine called DDAR (Deductive Database Arithmetic Reasoning).
The language model, trained on synthetic geometry problems, suggests potential steps and constructions that might help solve a problem. It does this by generating sentences in a specialized language that describes geometric objects and relationships.
DDAR then examines these suggestions, using logic to derive new facts from them. Following specific rules, it builds up what the team calls a "deduction closure" of all possible conclusions.
Iterative search process with knowledge exchange
The problem-solving process works through iteration. The language model generates possible next steps, which DDAR checks for logical consistency and usefulness. Promising ideas are kept and explored further.
A new search algorithm called SKEST (Shared Knowledge Ensemble of Search Trees) runs multiple search strategies in parallel, letting them share useful findings through a common knowledge base. This helps them work together and find solutions faster.
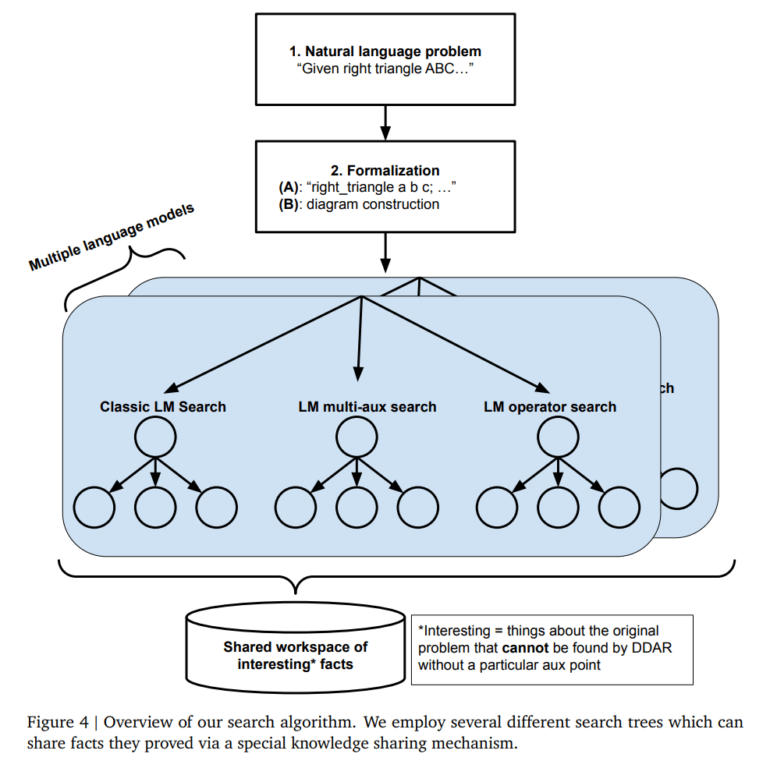
When DDAR finds a complete proof combining the language model's suggestions with known principles, AlphaGeometry2 presents it as a solution. The team notes that these proofs often show unexpected creativity.
Specialized tokenizers and natural language
Compared to the previous version of AlphaGeometry, many enhancements and optimizations have been made in the new version. These include a more expressive geometric description language that now includes locus curves and linear equations, as well as a faster C++ implementation of DDAR. The new version is said to be 300 times faster than the previous Python implementation.
Surprisingly, neither the tokenizer used nor the domain-specific training language play a decisive role in the performance of AlphaGeometry2. Similar results were obtained with both customized small-vocabulary tokenizers and generic large-model tokenizers. Training in natural language also produced comparable results to training in a formal geometry language.
Another interesting finding is that language models pre-trained on mathematical datasets and then refined on AlphaGeometry data acquire slightly different abilities than those trained from scratch. Although both learn on the same data, they develop complementary strengths. By combining these models in a new search algorithm called SKEST (Shared Knowledge Ensemble of Search Trees), the solution rate can be further increased.
Neuro-symbolic AI vs. transformer
The study also provides important insights into the role of LLMs in solving mathematical problems. According to the paper, it was shown that AlphaGeometry2 models are capable of generating not only auxiliary constructions, but also full proofs. This suggests that modern language models have the potential to work without external tools such as symbolic engines.
As far as can be seen from the work, the language models used have not yet been trained as reasoning models with the currently used RL methods - further performance improvements are therefore possible. It is therefore likely that the next version will rely more heavily on reasoning models and may reduce the role of the symbolic engine, at least experimentally.
The work on this showcase system for the performance of neuro-symbolic AI thus also reflects the central debate in current AI research: Can deep learning models reason reliably? Or more precisely: Can generative transformer models like LLMs learn to reason reliably? While AlphaGemeomtry2 clearly demonstrates the strengths of neuro-symbolic systems, the team's insights into the role of LLMs leave a conclusive answer open.
Limitations and use cases
Despite the impressive progress made, AlphaGeometry2 still has limitations. For example, the formal language used does not yet allow the description of problems with a variable number of points, non-linear equations, or inequalities. Also, some IMO problems remain unsolved. Possible starting points for further improvements are the decomposition of complex problems into subproblems and the application of reinforcement learning.
In addition to geometry problems, the approach could be extended to other areas of mathematics and science. Potential applications range from solving complex calculations in physics and engineering to assisting researchers and students.
Deepmind has previously achieved impressive AI results in Go, protein structure prediction and matrix multiplication with AlphaGo, AlphaFold and AlphaTensor - even winning a Nobel Prize for AlphaFold.
