Microsoft Research Asia has developed a training method called rStar-Math that enables small language models to match or exceed the math performance of much larger AI systems, such as OpenAI's o1-preview.
At the heart of rStar-Math is Monte Carlo Tree Search (MCTS), the same technique behind the success of Google Deepmind's Alpha Zero and similar systems. MCTS explores multiple solution paths and learns from the most effective ones.
What sets rStar-Math apart is its combination of plain English explanations with actual Python code. For each step, the model needs to both explain its thinking and write working code to validate its approach.
The researchers developed what they call a "code-augmented chain-of-thought" approach. The system expresses math concepts in both everyday language and Python code, with the code including detailed explanations as comments. If the code doesn't run properly, that solution gets rejected - essentially creating an automatic verification system.
This strict code checking is both a strength and a limitation. While it works exceptionally well for mathematical text problems where solutions can be clearly verified, it's hard to apply this approach to tasks without clear right or wrong answers, such as text comprehension.
The system also can't yet handle geometric problems because it currently lacks the capability to process visual information. However, the researchers see potential for this approach in programming tasks and common-sense reasoning, where similar verification mechanisms would work well.
Learning through self-assessment
The system uses a special evaluation model called the Process Preference Model (PPM) to assess each solution step. Instead of making yes-or-no decisions, it learns by comparing alternative solutions to identify effective approaches.
The training happens in four rounds, starting with 747,000 math problems. Both the main model and the evaluation model improve with each round, as the system creates verified solutions that help train the next generation of models.
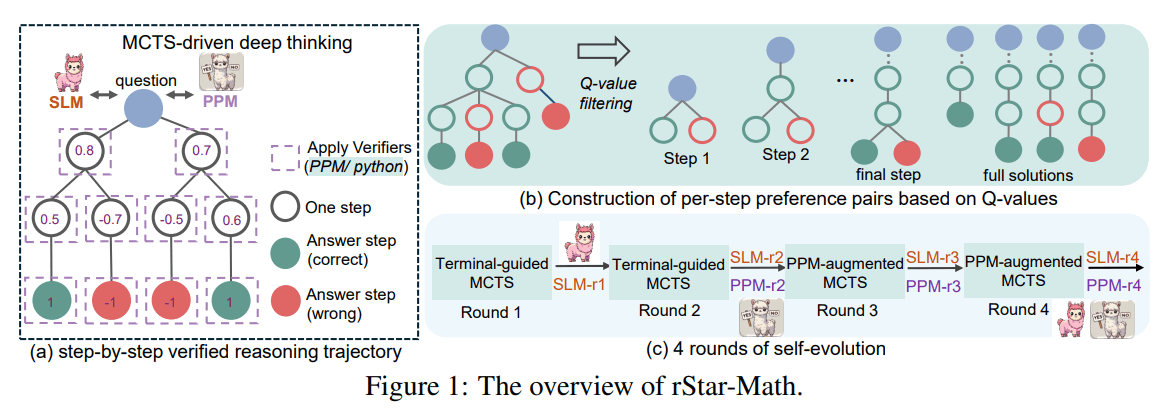
With each round, the system tackles increasingly complex problems and generates better solutions. What makes this approach different is that the system learns from its own successful solutions rather than copying answers from larger language models.
After training with rStar-Math, the 7-billion-parameter Qwen2.5-Math-7B model achieved 90% accuracy on the MATH benchmark - 30 percentage points better than its starting point and 4.5% higher than OpenAI's o1-preview. Even the smallest model tested, with just 1.5 billion parameters, reached 88.6% accuracy.
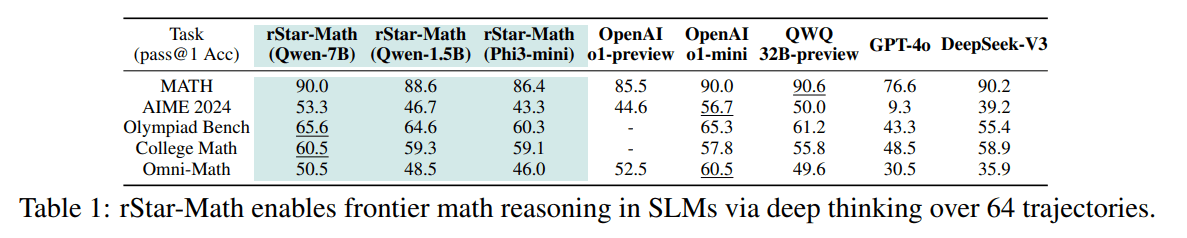
The system also performed well on the American Mathematical Olympiad AIME 2024, solving 8 out of 15 problems on average - matching the performance of the top 20% of student participants.
The Trade-Off: Computation Time
Like OpenAI's o-models, rStar-Math uses additional computing time during inference to try alternative solutions. The researchers specifically tested how well this so-called "test-time compute" approach scales for rStar-Math.
With just four solution attempts, rStar-Math outperforms o1-preview and comes close to o1-mini. Performance continues to improve as the system makes more attempts, up to 64 per problem.
However, the benefits vary depending on the type of math problem. For MATH, AIME, and Math Olympiad problems, improvements level off around 64 attempts, while college math problems continue to show gains beyond this point.
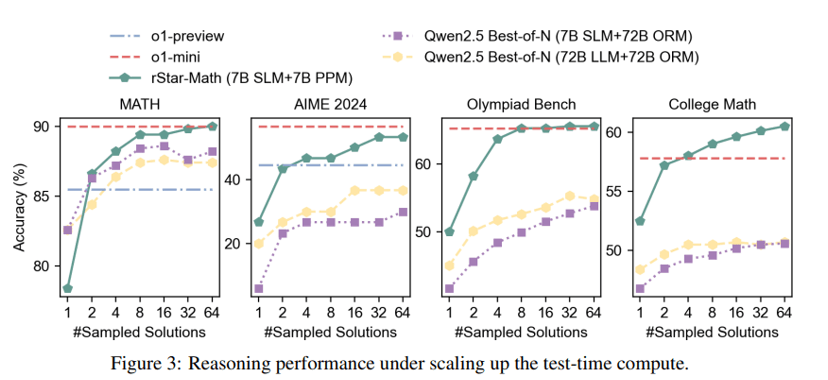
In addition to the difficult-to-generalize code verification system mentioned above, this is likely another limitation of rStar-Math. Test-time compute helps ensure accuracy and tackle more complex tasks.
But the need to run and evaluate dozens of solution attempts for each problem makes the process time-consuming and computationally expensive. The system's high accuracy comes at the cost of intensive processing, which is also the case with OpenAI's expensive o3 model.
Despite these limitations, the researchers emphasize that rStar-Math shows how small language models can create their own high-quality training data and improve themselves. They believe even better results are possible with more challenging math problems for training data.
Microsoft's focus on more efficient AI models
The development of rStar-Math fits into Microsoft's broader strategy to create smaller, more efficient AI models that reduce development and operating expenses. The company recently demonstrated this commitment by releasing their 14-billion-parameter Phi-4 model as open source under the MIT license.
The rStar-Math team plans to share their code and data with the research community as well. Project lead Li Lyna Zhang notes on Hugging Face that while they've already created a GitHub repository, it will remain private until they complete the internal approval process.
