Integrating the Monte Carlo Tree Search (MCTS) algorithm into large language models could significantly enhance their ability to solve complex mathematical problems. Initial experiments show promising results.
While large language models like GPT-4 have made remarkable progress in language processing, they still struggle with tasks requiring strategic and logical thinking. Particularly in mathematics, the models tend to produce plausible-sounding but factually incorrect answers.
In a new paper, researchers from the Shanghai Artificial Intelligence Laboratory propose combining language models with the Monte Carlo Tree Search (MCTS) algorithm. MCTS is a decision-making tool used in artificial intelligence for scenarios that require strategic planning, such as games and complex problem-solving. One of the most well-known applications is AlphaGo and its successor systems like AlphaZero, which have consistently beaten humans in board games. The combination of language models and MCTS has long been considered promising and is being studied by many labs - likely including OpenAI with Q*.
The Chinese researchers combine the exploratory capabilities of MCTS with the language models' abilities for self-refinement and self-evaluation. Both are essentially prompting methods where the language model's outputs are verified within its own context window. On their own, self-refinement and self-evaluation often bring only minor improvements, but they can be better supported in combination with MCTS. The result is the MCT Self-Refine (MCTSr) algorithm, which aims to improve the performance of LLMs on complex mathematical tasks.
MCTSr combines tree search with self-evaluation and back-propagation
The MCTSr method abstracts the iterative refinement process of mathematical problem solutions into a search tree structure.
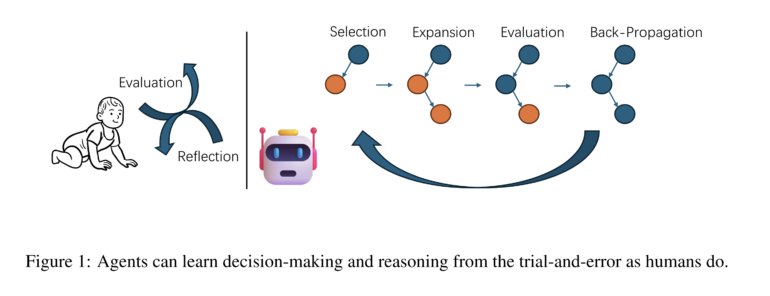
The algorithm consists of several phases: selection of the most promising node for refinement, self-refinement where the LLM generates feedback to improve the selected answer, self-evaluation to assess the refined answer through the LLM's self-reward, back-propagation to backpropagate the evaluation to the parent node and update the tree, and UCT update to select new nodes for further exploration.
MCTSr raises Llama-3-8B to GPT-4 level
The researchers tested MCTSr on various datasets, including GSM8K, MATH, and Math Olympiad problems. In all cases, the success rate increased significantly with the number of MCTSr iterations.
On the challenging AIME dataset, the solution rate rose from 2.36% in zero-shot mode to 11.79% with 8 MCTSr iterations. On the new GAIC Math Odyssey dataset, which according to the team has little overlap with the training data of the Llama-3 model used for the experiments, MCTSr achieved a solution rate of 49.36% compared to 17.22% in zero-shot mode. Overall, thanks to MCTSr, the Llama-3 model with only 8 billion parameters approached the performance of the significantly larger GPT-4.
The team now plans to test the method in other application areas.
